I would have asked this on a math community but I couldn’t find an active one.
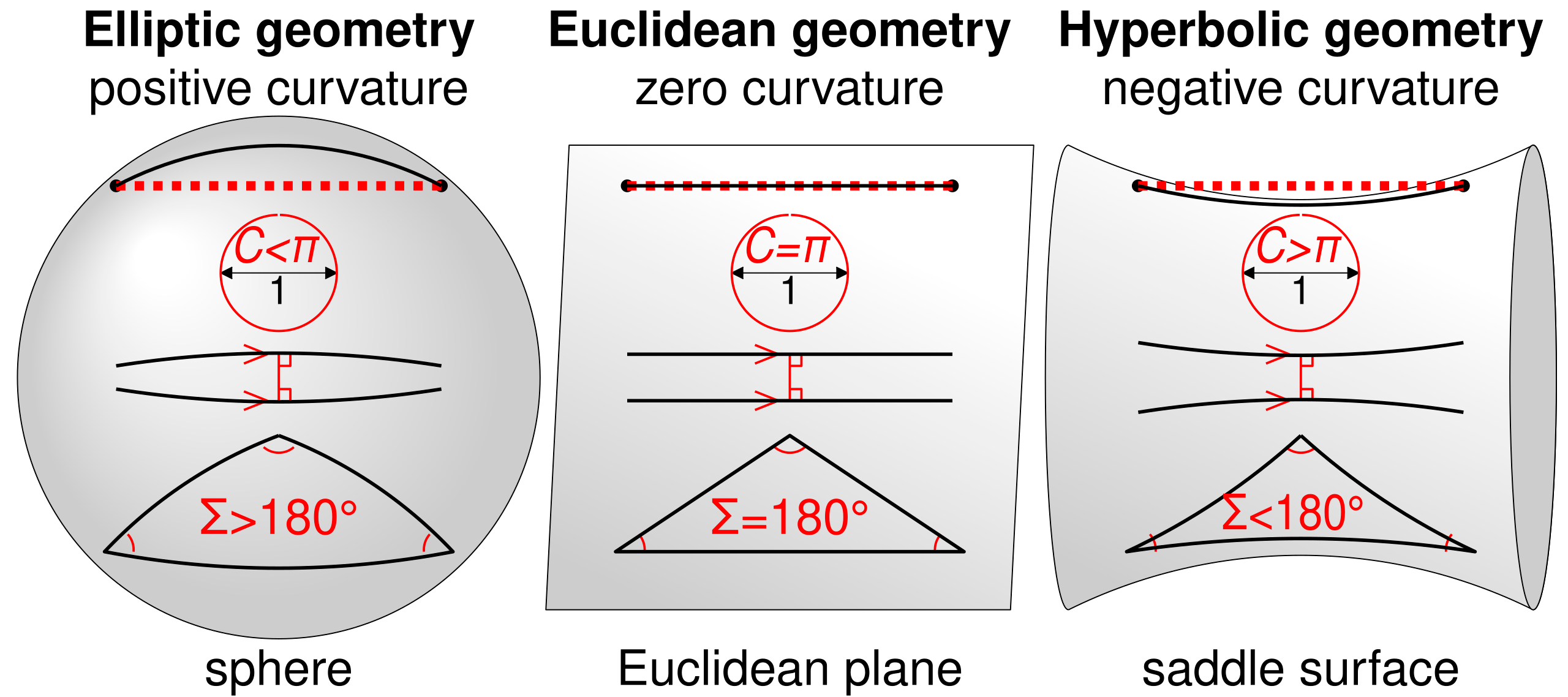
In a spherical geometry, great circles are “straight lines”. As such, a triangle can have two or even three right angles to it.
But what if you go the long way around the back of the sphere? Is that still a triangle?
(Edit:) I guess it’s a triangle! Fair enough; I can’t think of what else you would call it. Thanks, everyone.
Yes, but to be more specific, it is a spherical triangle.
Spherical isosceles triangle, in this particular example.
This is an example of non-Euclidean geometry. In this non-Euclidean space, it is a triangle.
I am pleased to see that there is a section on Lovecraft in that article. He really loved his non-Euclidian geometry
as well as being really aggressively racist
This inevitably comes up every time he is mentioned. Yes, he was very racist, even for the time. That mainly came forth from the fact that he was a very socially disturbed and scared person. Which isn’t an excuse, nu i think we should be able to appreciate the amazing writing and the influence he has had on the literary (horror) landscape without just focusing on the fact that he was racist.
What does that have to do with non-Euclidean geometry?
Don’t worry. Give it half a millenium and we all will have been racist against dogs.
It’s got three angles, so I’d say so
Oh so that’s why they call it that.
Just wait until you learn about the etymology of triceratops
It’s got three ceratops of course
Three knights can ride it; tri-sir-atop.



But there’s only one Michael Cera, how can this animal be topped with three of them!
Nah it tried to have three ceratops but it only got two of those things.
The wonders of non-Euclidian geometry. Yes, this is a triangle, but as it exists in a non-Euclidian space, some rules you learned about in school which mostly teach Euclidian geometry, don’t apply.
It is a triangle. The abstraction of lines in non-Euclidean geometry are geodesics and just like three lines form a triangle, so do the geodesics. If you walked along the earth’s surface from the equator to the North Pole and back, taking 90 degrees angles every time, you will have felt that you made a triangle by walking straight in three directions.
The reason the angle sum can be more than 180 degrees is that the sphere has a positive curvature. If you want one with negative curvature and less than 180 degrees angle sum, try to make one on the side of the hole on a torus (look up its curvature if my explanation was lacking).
EDIT: Picture for reference:
Would the southern shape here also qualify as a triangle?
What if you went the short way instead of the long way, creating the spherical triangle people usually use - then is the “outside” portion of the triangle itself another triangle?
Yes, that would be a different triangle. If you have 3 points on a sphere, there are multiple triangles that contain them as vertices.
I didn’t even think of that. Another good question!
deleted by creator
Yes, it has three corners and three edges. It is a triangle.
What if it had 3 corners and 4 edges? Or 4 corners and 3 edges?
If a shape has 3 corners and 4 edges, it is incomplete or open and therefore not a shape yet but a collection of edges (or possibly, two triangles that share an edge).
A shape with 4 corners and 3 edges is not possible. An edge cannot have a corner in the middle of it, that would make it two edges.
I felt like adding something about the specific case of 180° between edges and a vertice.
Makes sense.
And I guess too many vertices means an open set of edges (ie not close, this not a shape).
I was kinda hoping for a strange edge case, like a mobius strip or Klein bottle.I guess a mobius strip is a 2d representation of a 1d paradigm. And a klein bottle is a 3d representation of a 2d paradigm.
It would be too much to ask of a 1d representation of a ??d paradigm.
Why the down votes? Bro asking a question and being legit curious, don’t be hating on someone that’s looking to challenge what they know just because it’s trivial to you.
I feel my comment adds to the discussion and wants more details.
But it was too simply phrased.
I guess the details of such a question should be obvious. And if you need the details, the question doesn’t actually add the the discussion… It just seems idiotic!I felt like there might be a really cool scenario where a vertice isn’t considered a vertice.
Like, there actually might be some case on a 2d plane “where actually” applies.
I’m fine being wrongWelcome to Lemmy, first time?
I don’t think that can be a thing.
Yeh, seems not
It doesn’t matter that the edges are curved?
If you were to walk this route along the surface of the earth, you would walk in perfectly straight lines apart from the three turns.
No such thing. Even if you were walking on a surface with no change in elevation, the acceleration due to gravity would cause your path to be curved as it followed the curvature of the planet.
Curved relative to what?
Edit: Nvm, I understood what you mean. But I think it’s a pedantic take. They obviously mean it in the context of the surface of the sphere.
They’re not curved; the space they’re embedded in is curved.
The space itself has canonical curvature >.>
Well that depends on your definition of curved… If I look at this image from a 3 dimensional coordinate system that includes the sphere, the edges are definitely curved. Of course, if you look at this from the coordinate system “surface of the sphere” then I would agree with you. There are 2 ways to look at this and decide if it is a triangle, and the bro you responded to didn’t understand this and needs it explained.
I don’t think this is relevant. Using your first definition there is no possible way to walk in a straight line on a sphere. While true in that context I don’t think it’s what most people are meaning by “straight line”.
But it’s absolutely clear that the first definition is meant by the person that is being responded to. That is why the clarification is needed. This is not about “most people”, but this specific one person in this specific comment thread. “It doesn’t matter that the edges are curved?” is only said by someone that thinks in the first definition, not in the second.
The edges curve in 3d space, but not relative to the sphere.
There’s an entire field of science projecting shapes from the surface of a sphere onto a planar surface going back centuries.
Suffice it to say, I don’t know you’d have to talk to a map-nerd.
Just noticed in euclidean geometry, for any two line segments touching at a point there is exactly one triangle you can draw, i.e. a triangle is uniquely described by any two of its legs. In spherical geometry, there are two choices for the third leg!
Two things I need to ask:
- What inspired this question, exactly, and
- Can I have some, please?
I was reading Matt Parker’s new trigonometry book and they made some remark about triangles in spherical geometry and I went “wait, what if you did this”
There’s a theory about Alice in Wonderland that Lewis Carroll was satirizing the absurdity of the increasingly abstract mathematics that was popping up at the time. Now, I don’t think that theory holds weight–Alice in Wonderland doesn’t need to be anything other than a whimsical children’s book–but he did apparently write some things along those lines. This post is a pretty good example of something that would throw him into a rage.
Yes
Yes and I hate it >:(
Spherical geometry - good times…
Yep, it’s a triangle. You can also make one with three right angles on a sphere!
Doritos are triangles so sure
I’m not asking about a Dorito shape.
I’m sorry for your loss
The term you are looking for to describe such a shape is technically “spherical polygon”. Triangles are impossible in speherical geometry since the sum of the angles would always be greater than 180°.
There is no rule that the angles of a triangle add to 180 degrees. It only holds true in Euclidean geometry, which this is not.
There is no rule that the angles of a triangle add to 180 degrees.
I think this is debatable. If it was not, then the answer to OP’s question would be obvious, and this thread would be uninteresting. The words we use carry a lot of unwritten baggage.
I think OP clearly has an inkling of non-euclidian to even ask what they did, so I’m not sure euclidian rules are relevant to the discussion. It seems they know of it but non-euclidian geometry is not intuitive so this isn’t obvious to most.
The answer is obvious. Depending on the curvature of the object the triangles have higher or lower than 180 degrees angle sums. Flat space just happens to have 0 curvature.















